stataコマンド~欠損値処理にめっちゃ便利なmisschkコマンド~
おつかれあたん
stataユーザー作成のコマンドで特に便利と思うコマンドとしてmisschkというのがあります.欠損値は社会調査データにおいては切っても切り離せないコマンドで,分析それ自体よりも処理するための時間がかかるものです.
stataの場合,if文で処理するのが最も一般的であとはdropやkeepを使う方法などがありますが,misschkというコマンドを覚えておけば欠損処理がとても快適に行えます.
以下で使い方と便利なポイントを紹介します.
今回用いる架空例は下記のようにします.
| ID | y | x1 | x2 | x3 |
| 1 | 1 | 2 | 1 | 2 |
| 2 | . | . | 1 | 2 |
| 3 | 2 | . | 2 | 2 |
| 4 | 1 | . | . | 1 |
| 5 | 1 | 1 | 2 | . |
| 6 | 2 | 2 | 2 | 1 |
| 7 | 1 | 2 | 2 | 2 |
今回はyを従属変数,x1,x2,x3を独立変数として回帰分析や記述統計量,クロス表などを
作成したいとします.y~x3にはそれぞれ欠損値が存在します.ID番号が1,6,7の人は欠損値が一つもないため特別の指定をしない限り常に分析に含まれることになりますが,その他のIDは使用する変数や条件によっては分析に含まれないことになります.
以下で具体的な分析をみていきます.
まず,yを従属変数,x1,x2,x3を独立変数とするOLS重回帰分析を行います.
reg y x1 x2 x3
となります.このコマンドに代表される通常の回帰分析における分析対象は,「投入する変数がすべて欠損でない」ものに限定されます.つまり,IDが1,6,7の3人しか分析対象に含まれません.
上記のregの実行すれば,stataが勝手に欠損がある人を除外してくれるので大きな問題はありません.
しかし通常,分析に先立ち記述統計量を示すことが一般的です.
その場合sumというコマンドを実行するわけですが,仮に以下のようなコマンドを実行したとします.
sum y x1 x2 x3
すると,下記が出力されます
| Variable | Obs | Mean | Std. Dev. | Min | Max |
| y | 6 | 1.33 | 0.52 | 1 | 2 |
| x1 | 4 | 1.75 | 0.50 | 1 | 2 |
| x2 | 6 | 1.67 | 0.52 | 1 | 2 |
| x3 | 6 | 1.67 | 0.52 | 1 | 2 |
ここで問題となるのが,回帰分析におけるサンプルサイズと記述統計量で算出している各変数のサンプルサイズが異なる点です.通常sumを実行した場合には各変数ごとに欠損がない人を探しだしてきて記述統計量を算出します.たとえばx1についてはID1,5,6,7の4人が分析対象です.またy,x2,x3はサンプルサイズが同じであるため,一見同じ対象者であるようですが,データをみると,yはID2の人が欠損,x2はID4の人,x3はID5の人が欠損であるので,対象者が異なるわけです.
ここで,回帰分析に合わせて,ID1,6,7の3人だけを分析対象にしたい場合には,以下のようなコマンドを実行する人が多いと思います.
sum y x1 x2 x3 if y~=. & x1~=. & x2~=. & x3~=.
すると下記が出力されます.
| Variable | Obs | Mean | Std. Dev. | Min | Max |
| y | 3 | 1.3 | 0.58 | 1 | 2 |
| x1 | 3 | 2 | 0 | 2 | 2 |
| x2 | 3 | 1.67 | 0.58 | 1 | 2 |
| x3 | 3 | 1.67 | 0.578 | 1 | 2 |
このコマンドはy,x1,x2,x3がすべて欠損でない人だけを対象として記述統計量を算出してね,というコマンドであるので,まさに回帰分析の対象者と同じになります.その証拠にサンプルサイズがすべて3で統一されています.
また,回帰分析に先立ち2変数の関連をクロス表で見るということがしばしあります.
記述統計量の算出の時と同じように,サンプルサイズを統一したい場合には下記のようなif文を追加する必要があります.
tab x1 y if y~=. & x1~=. & x2~=. & x3~=.
tab x2 y if y~=. & x1~=. & x2~=. & x3~=.
tab x3 y if y~=. & x1~=. & x2~=. & x3~=.
すなわちすべて同じif文を設定してコマンドを実行することになります.
-----------
データ分析にある程度慣れた人ならここまでの話はある程度常識でありながら,いちいちif文を設定するのがとても面倒に感じているのではないかと思います.コピペするにしても,変数が条件が増えるほどコマンドが長くなってみづらいということもあります.
そこでmisschkコマンドが活躍します.以下実行例です.
まず,
search misschk
と入力してmisschkのプログラムをダウンロードします.
コマンドは以下のように入力します.
misschk y x1 x2 x3,gen(mis)
コマンドの意味は出力を見ながら説明します.
上記を実行すると下記のような出力が表示されます.
| # | Variable | # | Missing | % | Missing |
| 1 | y | 1 | 14.3 | ||
| 2 | x1 | 3 | 42.9 | ||
| 3 | x2 | 1 | 14.3 | ||
| 4 | x3 | 1 | 14.3 |
最初の出力はmisschkのコマンドの後に並べた4つの変数それぞれが欠損の数と割合を示しています.たとえばx1だと欠損が3つあり,全体のうち42.9%が欠損であるということを一覧表で示してくれます.この表を出力してくれるだけでもこのコマンドのメリットがあるかと思います.
次が欠損のパターンの出力です.
| Missing for | |||
| which | |||
| variables? | Freq. | Percent | Cum. |
| 12__ | 1 | 14.29 | 14.29 |
| _23_ | 1 | 14.29 | 28.57 |
| _2__ | 1 | 14.29 | 42.86 |
| ___4 | 1 | 14.29 | 57.14 |
| ____ | 3 | 42.86 | 100 |
| Total | 7 | 100 |
ここで,12__とは投入した変数4つのうち,最初の二つつまりyとx1が欠損の人が何人いるかを示してくれて,ここでは1人で全体のうち14.29%であることが分かります.
最後の____が,4つの変数がすべて欠損でない人の情報で,それは3人いて全体の42.86%であるという情報を示してくれます.この欠損のパターンを一覧で見れるコマンドはstataのデフォルトコマンドにはないためかなり重宝されます.しかも,この欠損パターンについては新変数としてデータセットに作成されます.
| Missing for | |||
| how many | |||
| variables? | Freq. | Percent | Cum. |
| 0 | 3 | 42.86 | 42.86 |
| 1 | 2 | 28.57 | 71.43 |
| 2 | 2 | 28.57 | 100 |
| Total | 7 | 100 |
最後出力が欠損の数で分類した度数分布表です.たとえば4つの変数のうち欠損が0に人が3人,欠損が1つの人が2人,という情報を示してくれます.
これらの表のうち,2つ目の欠損パターンと欠損の数の度数分布表から今回分析対象となるのが3人であることが分かります.
この表は回帰分析に限らず,欠損パターンの分析,たとえばyに回答しない人は他にどんな変数に回答しないのか,というパターンを示してくれるためかなり便利です.
そして,もっとも便利なのが,
misschk y x1 x2 x3,gen(mis)
のサブコマンドで指定した(mis)の部分で,データセットをみてみると,次のようになっています.
| ID | y | x1 | x2 | x3 | mispattern | misnumber |
| 1 | 1 | 2 | 1 | 2 | ____ | 0 |
| 2 | 1 | 2 | 12__ | 2 | ||
| 3 | 2 | 2 | 2 | _2__ | 1 | |
| 4 | 1 | 1 | _23_ | 2 | ||
| 5 | 1 | 1 | 2 | ___4 | 1 | |
| 6 | 2 | 2 | 2 | 1 | ____ | 0 |
| 7 | 1 | 2 | 2 | 2 | ____ | 0 |
ここで,mispatternというのは,先ほど説明したように,このサンプルがどういった欠損のパターンであるかを文字列として示されたものです.
そして,misnumberというのが,投入した4つの変数のうちいくつ欠損があるかを示した変数で数値として作成されています.
変数名は()で示した文字にnumberが足されます.たとえばgen(misA)と指定すれば
misAnumberのようになります.
この変数が作成される所がとても便利な所で,
先ほどまで,
sum y x1 x2 x3 if y~=. & x1~=. & x2~=. & x3~=.
tab x1 y if y~=. & x1~=. & x2~=. & x3~=.
tab x2 y if y~=. & x1~=. & x2~=. & x3~=.
tab x3 y if y~=. & x1~=. & x2~=. & x3~=.
と長いコマンドを指定していたと思いますが,
これをすべて,
sum y x1 x2 x3 if misnumber==0
tab x1 y if misnumber==0
tab x2 y if misnumber==0
tab x3 y if misnumber==0
と置き換えて分析することができます.
見た目もすっきりする上にmisschkのコマンドで様々な欠損パターンを作成を確認できて,その新変数を作成できるために重宝する場面は多いコマンドです.
stataコマンド logファイルの使い方とメリット
おつかれあたん
今回,logファイルの機能を用いてstataの出力結果とコマンドをまとめて確認する
ためのstataコマンドとその方法についてメモしておきます.
※このコマンドの通称が「log ファイル」なのか不明ですが,ここではそうします.
stataの欠点の一つとして,出力ファイルの編集が面倒だということがあると思います.
excelとの互換性に乏しいため,そのまま貼り付けようとしても,
行ずれや余計な空白ができたりして,それをいちいち修正するのは
かなり手間だったりします.
もし,論文などに表を掲載する場合は,面倒でもちゃんと修正する必要はありますが,
たとえば「ゼミの報告で使いたい」といった場面や「自分が後ですぐ確認できるようにしたい」というように,わざわざ成型された図表を提示する必要がない場面では
なるべく手間をかけずにわかりやすく結果を発表したいということがありえるかと思います。
そこで重宝するのが,logファイルです.
logファイルとは,(自分のざっくりした理解では)
「stataのコマンドを実行したときに出力viewに表示される結果を.smclという拡張子で
保存して,その出力を後で閲覧する機能」
になります.
使ったことがない人にはいまいち利点やイメージが伝わらないと思うので
(最初は自分も意味不明でした)仮想データを用いながら
コマンドも併せて説明します.
仮想データは下記のものです.
変数は
sex(性別:1=男性,2=女性),
age(年齢:20~40歳の連続変数)
job(雇用形態:0=非正規,1=正規)
income(収入:100~1000万の連続変数)
となります.
乱数を発生して作成しましたが,雇用形態とincomeが正の関連を
取るように,一部恣意的な入力を行いました.
さて,データを使って実際にdoファイルを作成していきます.
今回使用しているのはstata ver.16になります.
今回は収入を従属変数とした分析をすると設定し,以下のような分析を試みます.
①独立変数として使う「女性ダミー」変数を性別変数から作成
②雇用形態別に収入の記述統計量を出力
③女性ダミー,年齢,雇用形態を独立変数,収入(対数変換)を従属変数とした重回帰分析
となります.
(ふつう,収入は自然対数に変換しますが本筋ではないので無視してます)
実際のdo ファイルのコマンドはこんな感じです.
****2020年●月▲日作業*****
**データの読み込み
capture use "C:\Users\reata\OneDrive\デスクトップ\log_example.dta",clear
*****変数の変換
***女性ダミー変数作成
recode sex 1=0 2=1,gen(femaledummy)
*****収入を従属変数とした分析
***雇用形態別の収入の記述統計量
***正規雇用のほうが収入が高い
sum income if job==0
sum income if job==1
***収入を従属変数とした重回帰分析
**雇用形態のみ有意となった.収入や年齢が有意となっていないけど大丈夫か?
reg income femaledummy age job
本筋から逸れますが,コマンドの細かい確認です.
【データの読み込み:use】
データの読み込みはuseというコマンドになります.これで.dtaファイルが開けます.
フォルダからデータを探してクリックして開くこともできますが,
こちらのほうが後で説明する理由から便利です.
captureと先頭につけると,もしこのコマンドにエラーが出た場合でも,
続きのコマンドを実行してもよい,という命令になります.
(ふつう,stataはコマンドエラーが出ると続きのコマンドが実行されない.)
このcaptureはuseに限らずあらゆるコマンドの先頭につけることができますが,
特にuseコマンドの前につけると便利なことが多いです.
というのも,個人が複数のPCを用いてstataのコマンドを書いているor共同研究者と異なるPCでstataのコマンドを共有しあっているといった場合に、
一つのdoファイルの中に,
capture use・・・
capture use・・・
というように,AさんとBさんの複数のディレクトリを示しておけば,
どちらか一方のディレクトリが正しく示されていればデータを読み込むことができる
ため大変便利です.また,doファイルの保存場所さえ覚えておけばデータの保存先と
データ名はdoファイルにメモされているため記憶の節約ができると思います.
ちなみにディレクトリとはコンピュータの中の住所だと思ってもらえれば問題ないです.useの後の" "で囲まれた中に実際の住所を指定するわけですが,
簡単にいってしまえば,
"日本:東京都\文京区\本郷\東京大学"
のように\の後ほど下層の住所を指定していく感じです。
オプションのclearはすでに,stata内に別のデータが読み込まれていて,それが
保存されていない状態であっても,そのデータを保存しないで新しいデータを読み込ませる,という命令になります.
さて,上記のコマンドを実行すると次のような出力が出てくると思います.
(スクショで貼り付けてます.)
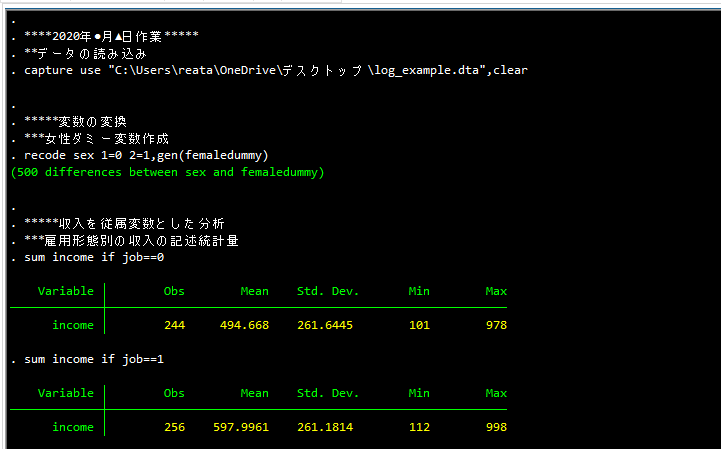

もし,上記のような結果をすべてゼミ報告をしたいという場合,
これらの結果をexcel等に一つずつ貼り付けて,それを編集して,最後にwordファイル等に貼り付ける,といった手順を踏むことが多く,かなり面倒です.
そこで,log ファイルというものを活用します.
下記のようなコマンドです.
*****log ファイル*****
cd "C:\Users\reata\OneDrive\デスクトップ"
log using result2020income,replace
****2020年●月▲日作業*****
**データの読み込み
capture use "C:\Users\reata\OneDrive\デスクトップ\log_example.dta",clear
*****変数の変換
***女性ダミー変数作成
recode sex 1=0 2=1,gen(femaledummy)
*****収入を従属変数とした分析
***雇用形態別の収入の記述統計量
***正規雇用のほうが収入が高い
sum income if job==0
sum income if job==1
***収入を従属変数とした重回帰分析
**雇用形態のみ有意となった.収入や年齢が有意となっていないけど大丈夫か?
reg income femaledummy age job
log close
***************************************
logファイルを実行する前にはまず,cdというコマンドを実行します.
cdとは,change directoryの略です.
ディレクトリは前述したとおり,コンピュータの住所になります.
cdの後の" "の中に住所を指定し,
今回の例でいえば,最終的にはデスクトップを指定していることになります.
その後のコマンドがlogファイルを取るコマンドとなります.
まず,log using までが「logファイルを記録しろ」というコマンドで,その後のresult2020incomeはファイル名となっています.
つまり,「result2020incomeというファイル名でログを記録して,それをデスクトップに保存しろ」というコマンドを実行したことになります.
オプションのreplaceも重要で,これを入れると上書き保存になります.
replaceを入れないといちいち,ファイル名を変更しなければなりません.
(すでに存在するファイル名です,というエラーが表示されるため).
書き換えない場合はもちろん,replaceをとって,ファイル名を変更してください.
そのため,ここは各自のPCの環境に合わせてディレクトリを変更する必要があります.
そして,重回帰分析を行ったコマンドの最後にlog closeというコマンドを入力します.
これは,文字通り「logファイルの記録を終了します」
というコマンドなのですが,これはlog usingと合わせて使うコマンドであって,
「log usingからlog closeの間に挟んでいるdoファイルの実行結果のログをすべて記録しろ」
という命令になります.
ここまでlogファイルと繰り返し言ってきましたが,実際何が起きているのかよくわからないと思うので,実際の画面で確認してみます.
まず,上記のコマンドをstataですべて実行してみます.
するとstata上の出力ではlog usingのコマンドを実行する前と
特段変わったところはなさそうです.
次にcdで指定したディレクトリ先に行ってみます.今回の例だと,デスクトップです.
すると,下記のように「result2020.income.smcl」というファイルが作成されていることが分かります.

これこそがlogファイルの正体です.拡張子はデフォだと.smclとなっています.
これを開くと下記のような画面が出てきます.
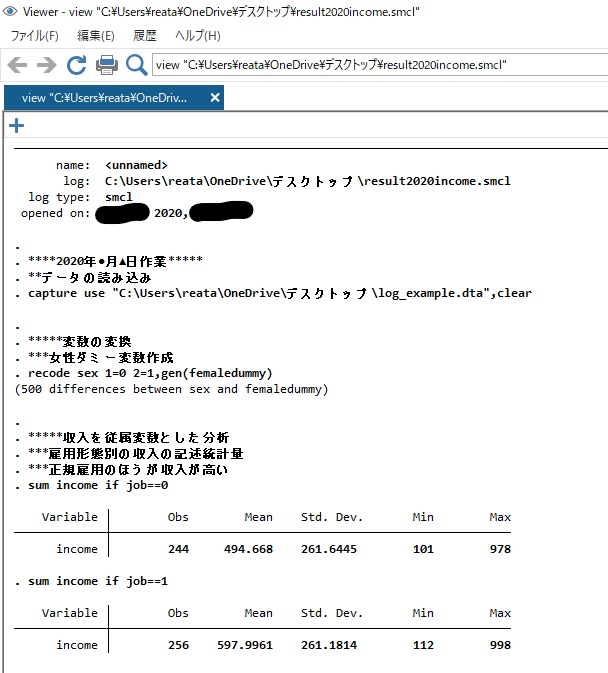
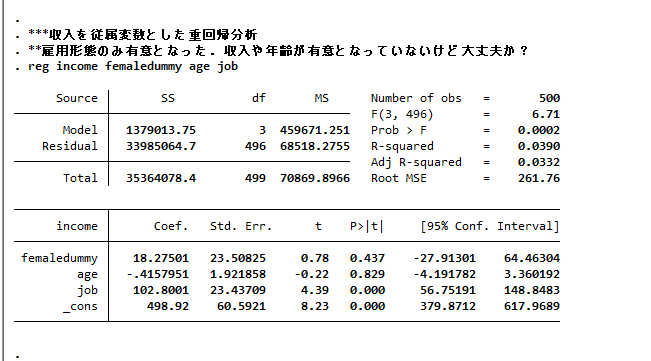
これは,log using とlog closeで囲まれたdoファイルのコマンドを実行した
結果,stataの出力画面に表示されたすべての情報を記録したものとなります.
これの便利なところは,例えばゼミの場面でこの画面を見せれば
その人がどういった変換をして結果を出したのかすぐ分かるし,
かつコメントを残しておけば,どういった手順で変数の変換をして出した結果なのか,
どういった点が気になっているのか,などを実際の結果と合わせてみることができる
点にあります.
今回女性ダミーという変数を作成しましたが,もしこの変換がおかしい場合なんかには
結果の表と見比べてながら「このコマンドがおかしい」というコメントをもらったり,
過去のログファイルを開けばいつの時点でコマンドが間違えていたのか,振り返ることもできるわけです.
またopened onというところには,logファイルを取った日時が記録されているため,
この分析がいつの時点のものかも知ることができます.
使い方は色々ですが,いずれにせよ,わざわざエクセル等で図表を編集して提示する手間が省けます.
ディレクトリの指定など,慣れるまでは少し面倒なところがありますが,
とても便利な機能です。
xrlogitとgllamm
おつかれあたん
xtliogitとgllammで2値の従属変数についてランダム効果を推定した場合,なぜか結果が違うことがあり,その理由がたまたまPower and XieのStatistical methods for categorical data analysisを見てた時にわかったんですが(P125注釈),xtlogit ではapproximation methodを用いるが,gllammでは,quadrature rulesで推定を行うためということでした.すごく細かくてささいなことですが,メモです.
がんばれあたん
リンク関数について
おつかれあたんです
よく一般化線形モデル(Generalized linear model)を説明する際にしばしば出てくる「リンク関数」という言葉を自分もよくわからんままスルーしていた時期があり,同じようにいまいち理解していない人もいるのかなと思うので,いちおう自分の理解をまとめています.
まず一般化線形モデルとは,ざっくり言えばいわゆる残差を任意に設定できるモデルことです.つまり,いわゆる最小二乗法(OLS)線形回帰やロジスティック回帰,プロビット回帰,ポアソン回帰などがすべて一般化回帰モデルの一族といます.名前が似ているものとして,「一般線形モデル」というものがありますが,これはいわゆる最小二乗法に従うモデルのことで一般化線形モデルの一つです.
具体例として,ロジスティック回帰分析を考えてみます.ロジスティック回帰分析は従属変数が2値,つまりは1か0をとるときに用いる手法です.多くの統計分析の教科書にあるように,こうした二値の値を取るような事象(表か裏か,成功か失敗かなど)はベルヌーイ分布(二項分布)に従うとされています.その中でも特にロジスティクス分析に従うものをロジスティック回帰分析と呼びます.
ここで最初のつまずきポイントになるのが,さっき「ベルヌーイ分布に従うといったのになぜロジスティック分布が登場するのか」という点だと思います.
まず,「ベルヌーイ分布に従う」の部分について説明します.ここでいう「ベルヌーイ分布に従う」とはあくまでY(従属変数)の分布のことを言っているわけです.ロジスティック回帰分析はYが1か0かをとる事象を確率分布として示すことができますが,これがベルヌーイ分布に従っていると定めていることになります.
重要な点はXの値に関係なくYの分布だけ見た時にどうなっているか,を考える点です.
たとえば社会学だと,結婚しているか否かという分析を行う際に「結婚を1,未婚を0とする変数の分布形は何か?」ということを考えることになります.これはまさにYの分布を考えているわけでたとえば,「ベルヌーイ分布に従う」と設定して分析を行うわけです.
もちろんベルヌーイ分布に従うという仮定がいつでも正しいわけではないため,二項分布がおかしな場合には別の分布形を考えていくことになります.
次にリンク関数です.これは,「XとYの関係を示すのに最適な分布は何か?」と考えることに他なりません.たとえば,あるデータについてYの分布をベルヌーイ分布を仮定したとします.そして次にXとYの関係をロジスティック分布で表す,ということになります.
ここでは図示しませんが,ネットで「ロジスティック分布」,と検索すれば,どんな分布かすぐに出てきます.その特徴としては,
①範囲が0~1に収まる(OLSではこの上限下限がない点で大きく異なる)
②曲線で,単調増加(Xが増加すると,Yは常に増加する).
③Xが小さい時はYの増加も小さく,Xが中間点ではYの増加も大きく,また,最後にYの増加が小さくなる.
というような形をしています.特に①がOLSとの違いとして強調される点です.
先ほどの具体例に即するならば,結婚できるかどうかという確率は,年収によって異なる,とするならば,Xを年収,Yを結婚とする分析になるわけですが,
この「年収と結婚(確率)の関係をロジスティック分布として示す」ということになります.
ここで,重要なのはYがベルヌーイ分布に従えばそのリンク関数は必ずロジスティック分布である,というわけではないということです.あくまでも「ベルヌーイ分布の特徴に加えXとYの関係を示す際のロジスティック分布の①~③の特徴を考えると,OLSよりも当てはまりが良さそうな分布形だな」,ということを考えて分布形を設定しているにすぎません.
つまり,XとYの関係を示すリンク関数として(累積)正規分布を仮定してもよいわけです.リンク関数として(累積)標準正規分布を仮定する場合がプロビット分析,というわけです.
ちなみに,ロジスティック分布と(累積)正規分布はかなり形状が似通っています.共通点は①で言ったように0~1までにどちらも収まるということ,さらには②と同様に単調増加です.相違点は曲率です.つまりは,Xが1単位増加した時のYの増加分はロジスティック分布と(累積)標準正規分布では少し違っています.
最初にもう一度戻して考えると,リンク関数とはXとYの関係を示す分布のことであって,このリンク関数を任意に設定できるものが一般化線形モデルである,と理解することができます.
個人的な印象としてはここまで理解するのに3ステップあるのかなと思います.
1ステップ目が「Yが0か1かの場合にはロジスティック分析かプロビット分析を用いる」
ということを理解しているか,
2ステップ目が「Yがベルヌーイ分布に従う」とはどういうことが理解しているか,
3ステップ目が「それぞれのリンク関数はロジスティック分布と(累積)正規分布に従う」ということをリンク関数という言葉の意味を含めて理解しているか,
という3ステップかなと思います.SPSS,STATA,SAS,Rなどの統計ソフトを回すだけであれば,1ステップ目さえ理解しておけば大きな問題はないと思いますが,近年増えてきた一般化線形モデルやその先に進むには,3ステップ目まで理解しておくことが必須になるのかなと思っています.
ちなみに近年では1段階目にあるようにYが0か1かの場合にいつもロジスティック回帰やプロビットを用いることに疑義が向けられており,OLS回帰を用いるような例もあるため注意も必要です.
がんばれあたん
観測データ(列数)の上限を増やす方法~stata~
おつかれあたん
stataを使って観測データの上限を増やす方法です.
使いどころは主に経年調査のデータを合併するなどした場合に変数の数が滅茶苦茶増えた時です.
例えばパネル調査で第10波まで達するような場合,変数の数が余裕で1万を超えてくる
ようなことがあります.そうした場合,デフォルトだとデータを読み取ることが
できません.
ちなみにstata15ではデフォルトの変数数の上限は,ICが2,048,SEが5,000,MPが5,000となっています(ラインストーン社サイトより).しかしそれぞれの最大上限をICは2,048,SEは32,767,MPは120,000まで拡大することができます.
※ICは変更できません.
コマンドは
set maxvar 10000
10000のところは任意の数値で上記の場合,読み取れる最大の変数数が10000となります.ちなみに,デフォで読み取れる変数の数が少ないのは,PCのメモリの関係上,負担が少ないよう少なめに設定してあると書いてました.要するに弱っちいPCでもstataの起動や分析の際に固まらないようにするため.
また,サブコマンドを付けて
set maxvar 10000,permanently
とすると,設定を保存でき次回以降開いた際も10000で読み取ることが可能になります.
がんばれあたん
ロジットとプロビット
いわゆる1か0かの選択,例えば大学に合格したか否か,あるいは現在幸せか否か,などの2択がどんな要因によって決定されるか分析する際には二項選択モデルをことが一般的です.代表的なのはロジット(ロジスティック)分析(以下ロジット分析),プロビット分析.これらの分析について両者の違いにも言及しながらなるべく簡易な説明を行います.今回は数式を使って説明しますが,なるべく簡単かつ数式がわからずとも理解できるように.
今回の従属変数はとします.iはある値でyが条件づけられることを指します.たとえばi=1の時のyの値,i=2の時のyの値…というようにiの値によって,yが変わりうることを指しています.こうしたある値によって注目する値(ここではy)が変わりうることを(yの)条件付き分布と言います.この辺りは二項選択モデルでなくとも当てはまる考え方です.ここでyはが何かを選択すれば1,選択しなければ0となります.普通のOLS回帰の場合はこのyの値の範囲が0より小さい値や1より大きい値をとるわけです.こうした1か0かをとりうる確率モデルはベルヌーイ関数として定式化が可能です.ここでは数式での理解よりも,より実践的な場面での理解や注意点を目指した説明を重視しますが,こちらの式は(教科書や分野によって多少変形するものの)よく出てくるので,理解しておくことを推奨します.今回は,北村(2009)ミクロ計量経済学入門(日本評論社)を参考にしています.さて,ベルヌーイ確率関数は以下のように定式化できます.
ここで, の省略形です.この省略形の式は,ある個人iのxがある値をとる時,その個人iの値yが1となる時の確率という意味です.1との間の縦線はその線の右側の値で条件づけた時に左側がどうなるか,という感じのニュアンス,Prは確率(Probability)のことです.そして,肝心のの式について訳していくと,はxで条件づけられた時のyの関数は…となります.fは関数(function)も意味.そして,右辺の第一項は先ほど説明した通り,二項のはy=0となる確率のことです.1か0かしか取り得ない確率の場合,例えば大学に行ける確率が80%なら,行けない確率は1-0.8=0.2で20%となります.引いては,0か1かしか取り得ない値の分布,つまりベルヌーイ分布は0になる確率と1になる確率の積で示すことができるということです.そして,その期待値(平均)をとすると,
=1×+0×(1-)=
となります.ちなみに分散は,(1-と表すことができます.
さて,最小2乗法でもそうですが,よくある回帰分析ではこの平均を求めることが一般的な手続きで,様々な統計パッケージの出力も基本はこの平均値を出力してくれます(もちろん分散も).この期待値は先ほど何度もxを出していたようにふつうは変数で説明され下記のように表します.
となります.この意味は,を変数xとその係数βで説明しようくらいの意味です.そして,このの定式化によってロジット分析かプロビット分析か名前が変わりうるのです.これをロジスティック分布とする場合はロジット分析,標準正規分布とする場合はプロビット分析と言います.難しいテキストとのかけ橋のために丁寧に説明すると,ロジット分析では確率分布をベルヌーイ分布(二項分布)でリンク関数をロジスティック分布とする分析で,プロビット分析では確率分布をベルヌーイ分布(二項分布)でリンク関数を標準正規分布とする分析です.
確率分布とリンク関数とは?となる人もかなり多いと思いますので(私は最初チンプンカンプンだったので)説明すると,確率分布はいわゆる従属変数yがどういった分布に従うのか想定するもので,今回の例でいえば1か0かをとるので,こういった分布の場合にはベルヌーイ分布を用いることが最も一般的です(もちろん他の分布もありますが).ただし,当然ながら注目するyは平均と分散を持っているわけです(もし平均や分散,つまりはyの値に違いがなければその違いを予測しようという話にはならないわけなので).そしてこのyの値はもしかするとxの値によって変化しうるのです.具体的にはyの値はxの値によって直線的に上昇することもあれば,xが小さい時はyも小さいがxが大きくなるにつれてyが非直線的に急上昇することもある,という話です.直線的な変化を予測できる場合にはリンク関数は直線でよいわけですが(これを恒等リンク関数といいます.一般的なOSLの際はこれです),非直線的に上昇する場合には別の関数が必要です.二項選択モデルの時の代表的なリンク関数がロジスティック分布(ロジット分析),標準正規分布(プロビット分析)といいます.
ここで話を少し戻して,先ほどのを微分したものがxの効果ですが(説明略),これを微分したものをとします.ここで,lは説明変数xのl番目の要素つまりはxの値であることを示します.ここでとても重要なことはxの効果を表すこの式に,lという添え字がついていることで,つまりはxの値によって係数βの値が変わりうるということです.これはOLSとの大きな違いです.少しくどいですが丁寧に説明すると,これはxのどの値で偏微分するかによってβの値が変わるということ,それはOLSが線形であり二項選択モデルが非線形であるから,という理由です.また,これに合わせて,ロジット分析とプロビット分析の違いにも触れていくと,両者とも同様に非線形,つまりは関数が曲線なのですが,その曲線の形状(曲率)が違うために,同様にxが一単位増加した時(たとえばxが1→2に増加したとき)の係数値を比較することができないことになります(曲率の違いはネット検索で出てきます).
さて,もう一度xの効果であるβについて考えてみます.また難しいテキストとの橋渡しのために,このxの効果を平均限界効果(marginal probability effect)と言います.限界〇〇は経済学の入門的な用語でつまりは一単位変化した時に注目する変数(ここではy)がどれくらい変化するか,というものです.先ほど述べたようにはl番目の要素によって限界効果が変わりうることを述べましたが,添え字iもあるので,iによっても限界効果が変わりうるのです.これをより簡単にいうと,例えば塾に通った年数が1年→2年の時と2年→3年の効果は同じ1単位でも違うし,しかも1年から2年通った時の効果は男性と女性という別の要素によっても変わりうることを示しています.そこで何とかして値を一意に評価する方法はないか,ということで,限界効果を次の2つの方法で評価することがあります.
第一が平均限界効果(AMPE)です.次のように示します.
この式が示すことは,上記のすべての個人iの平均を限界効果として代表するという方法であり,そのためにn番目の個人の効果の合計をnで割っています.解釈としては,「xが1単位増加した時に全体として平均的にどう増加するか」を示します.
次が期待限界効果(EMPE)という方法です.次のように示します.
EMPE=
これは,平均的なxをとる人の値が1単位増加した時の効果を示しています.
ちなみにstataでの平均限界効果の出力は,通常のロジット,プロビット分析の後に
margins,dyxy(*)
期待限界効果は,
margins,dyxy(*) atmeans
と入力します.
潜在成長曲線モデルメモ~stata~
潜在成長曲線モデリングはざっくり言えば,パネルデータ分析とマルチレベルとコラボした分析(と自分は理解してます).
パーソンレベルデータやワンショットの分析)の場合のマルチレベル分析は,レベル2が地域や学校,クラス,時代(コーホート)といった特定の個人が属するグループ変数,レベル1が個人を示す変数でたとえば,ある生徒が学校にネストされている構造を仮定する.
ネスト構造を仮定するとは,個人の社会経済的地位や意識などはその個人が属する集団の影響を受けているという話.学校の例でいえば,ある生徒の学習能力(成績)は,進学校にいった場合とそうでない場合にまったくその伸びが違うとか,あとプロスポーツ選手の例でいえば仮に全く同じ成績を残したとしてもジャイアンツにいるのと広島カープにいるのでは年収が全然違うとかといったイメージである.
また,このネスト構造は必ずしも2段階に限定されず3段階(レベル3),4段階・・・と考えられる.たとえば,ある個人がクラス,学年,学校,市町村,さらには都道府県,さらには,日本,アジア,ユーラシア,南半球,地球・・・などネスト構造はどんどん考えられるが,推定も重くなり,さらに構造が複雑になりすぎるので高次の構造はあまり考えない. ほとんどがレベル2まで.一度だけレベル3の構造を仮定したものを見たことがあるが,正直解釈が複雑でよくわからなかった...
さて,パネルデータのマルチレベルの際には,ふつうレベル1にある個人がレベル2にいる.そして,レベル1にはある個人の各時点ごとの状態が入る.たとえばA君の高校1年生の時の成績,2年生の時の成績・・・のようなパターンである.当然ながら,成績というのはそれぞれの個人の中で何かしらの関連を持っていることが想定される(たとえば1年生の時に勉強を頑張れば2年生でも成績が良いとか)ため,ネスト構造を仮定することができる.
さらにパネルデータのマルチレベル分析の特徴としては,ある個人の各時点での状態というのは,時間に依存した関連を持っていることが考えられる.先ほどの成績の例を見ても,高校2年生の時のテストの成績は前年のテストの成績と関連をもっていそうだし,さらにいえば2年前の中学3年生の時の成績とも関連をもってそう,というように,各時点の情報が連なって関連を持つことが想定される.当然ながら,そうしたパターンが見いだせないこともある.この個人の関連,固い統計用語でいうながば,レベル1の誤差の分散共分散構造に何かしらの相関パターンを想定した分析を行うこととなる.
本来ならば,固定効果,ランダム効果(切片and傾き),交互作用などもまとめておいたほうがいいが,ここは省略.
stataのコマンドは以下の通り.mixedというコマンドで,もしロジスティック回帰分析を行う際にはmelogitを用いることになるが,全然計算が収束しないので,試したモデルがまずいのか,やはりロジスティック回帰分析の計算はそうとうきついのか,どちらかだと思う.
・まず,下準備としてreshapeによって,パーソンピリオドデータに変換しておく必要がある.これによって,1レコード(1行)は,ある個人のある時点における情報が並ぶことになる.
その上で,レベル1,レベル2の分散共分散のみを出力するコマンド
mixed y || id:
yは従属変数idは個人を示す変数.これによって,yを説明する全体の分散を個人間の違いで説明できる分散と個人内の違いで説明できる分散とに分ける.もし,これで個人間の違いを説明する分散が極端に小さい場合には,わざわざマルチレベル構造を仮定する必要はなく,つまりはレベル2を仮定する必要はなく,レベル1のみ(つまりは固定効果のみ)で分析をすればよい.その場合には固定効果モデル(xtreg)というコマンドが使える.
(このあたりの説明も機会あれば少し丁寧にまとめたい). ちなみに,上記のコマンドを実行すると,本当にレベル2構造を仮定していいのかどうかの検定をやってくれて,出力の一番下にLR test vs. linear modelとあるので,そこで有意ならレベル2構造を仮定したほうが良いよね,というお墨付きをもらえることになる.出力の下に
Random-effects Parametersと出てきて,var(_cons)が個人間の分散,var(Residual)が個人内の分散である.また,出力のすぐ上に_consとあり,ここによく見る出力があるが,そのCoef.すなわち切片の値が,var(_cons)のEstimateの幅を持っているということが示されている.もう少し具体的にいうとyを成績を考えて,_consは調査の最初の時点での全個人の成績の平均ということになる.しかし,当然ながらスタート時点での成績は個人間で変わりうることが想定されるため,var(_cons)のEstimateの幅をもっている,ということになる.
mixed y || id:time
次にレベル2にtimeという変数を投入する.これは,時間変数で,たとえば調査を15,16,17歳と行うのであれば年齢の変数が入り,2018,2019,2020と1年ごとに調査を行うのであれば,年数の変数が入る.出力の中に,var(time)が増えているが,これは,レベル2の傾きのランダム効果となる.成績の例でいえば,当然ながら個人の成績は毎年伸びたり下がったりするわけで,つまりはある程度傾きをもっているわけであるが,成績の伸び方は各個人で全く違うわけである.たとえば成績が悪い子が急上昇するかもしれないし,成績が良い子はあまり伸びないまま一定であるかもしれない.そうした構造を仮定して,レベル2の傾きの分散を推定する. 簡潔なモデルを目指す場合あえてレベル2の分散を推定しないこともあるが,手順としては,一応踏んでおくのが良いと思われる.
mixed y time || id:time
次に,レベル1にtimeという時間変数を追加してtimeの固定効果を推定する.解釈は切片の時と同様で,個人の成績の変化の平均的な傾きは固定効果で求められた推定値となるが,それがレベル2(先ほどのvar(time))くらいの分散をもって傾きが変わりうることを想定することになる.
また,傾きのランダム効果を仮定することの統計的妥当性は,lrtestというコマンドで確認できる(中でどんな処理をやっているかはちゃんと調べてないので,調べる必要あり).ながれとしては,
mixed y || id:time
estimate store random_constant
mixed y time || id:time
estimates store random_slope
lrtest random_constant random_slope
とすると,尤度比検定が実行され,有意であれば,傾きのランダム効果(ランダムスロープ)を仮定することの妥当性が支持されることになる.
mixed y time || id: time, covariance(unstructured)
次はレベル2残差にどういう関連(分散共分散構造)を仮定するかというコマンド.
レベル2はつまり個人間の成績に何か関連が見いだせそうかという話で,いくつかパターンが考えられるが,ここは通常,何かしらの構造を仮定しないことが多いためcovarianceの()の中は,無相関を仮定するunstructuredを入力することが多い.つまりは,各個人それぞれに異なる分散の構造を推定することになる.また,分散が全く同じである一致(identity)を仮定することも多い.これらも色々試してみて,上記のlrtestやestat ICなどによってどのモデルが最適か判断するのが良い.
mixed y time || id: time, covariance(unstructured) residuals(ind)
次は,レベル1残差にどういう関連(分散共分散構造)を仮定するかというコマンド.これは最初の導入で説明した,今の成績は前の時点の成績と関連するよね,という話.どういう関連を持たせるか,いくつか代表的なものがあるが,簡単.residuals(identity)が同一で,これは,ある個人の各時点の残差の分散がすべて等しく,かつ各時点間の分散には関連がないことを表す.次に対角residuals(diagonal)は各時点の残差は異なるが,各時点間の分散には関連がないことを表す.次にresiduals(unstructured)は,残差も各時点の相関の仕方もすべて異なるという仮定である(つまり,全パラメータを推定することになるので,少し重たくなる).次に,residuals(ar1,t(time))は,は,各時点の残差の分散は同じで,各時点の相関を見た時に,時点によって何かしらの相関が見いだせそうなパターンである.たとえば,今の成績が1時点前と強く相関するが,2時点前との相関は少し弱くなり,3時点前はさらに弱くなり・・・というように何かしらの関連をもって相関が強く(弱く)なり,ar1とした場合は1次の自己回帰といって,1時点前後で相関が強く残り,2時点,3時点となるとある規則性をもって関連が弱くなることを想定している.個人的にはこれがけっこう好きで,かつ割と最適なモデルにもなりやすい気もする.次にresiduals(toeplitz)で,各時点の残差の分散は同じで時点が離れていくと相関が異なる(弱くなる)ことを仮定している.一次の自己回帰との大きな違いは,そこに規則性(パターン)がないため,たとえば,一次の自己回帰だと,相関は時点が遠くなると相関が一定の規則で弱くなるようなことを仮定するが,こちらは,次第に弱くなった関連が突如強くなるようなことも仮定している.そのため一次の自己回帰よりも少しパラメータの推定が多くなる.その他,いくつかあるが(exponentialやexchangeable),省略.また,もちろん自分で分散共分散行列を作成することもできる.
mixed y time || id: time, covariance(unstructured) residuals(ind), reml
制限付き最尤法(reml)によって推定を行うコマンド.詳しくないので,後日勉強.
mixed y time x1 x2 || id: time, covariance(unstructured) residuals(ind)
今までの説明は,パネルデータにランダム構造を仮定して良いかどうかの話がメインで,そこが固まればようやく説明変数を投入していくことになる.普通の回帰分析同様にyの後にレベル1の独立変数を投入していく(固定効果).
mixed y time x1 x2 time#c.x1 || id: time, covariance(unstructured) residuals(ind)
時間変数と独立変数との交互作用をとる.要するに,注目している独立変数の効果が時間によって変わりうるのか検証する.これは通常の回帰分析の解釈を応用できる.仮にx1を女性ダミー変数と考え,主効果が正でかつ,交互作用効果が正であれば,女性は平均的に成績が高くなりやすく,かつ時点を経ると成績の伸びは女性のほうが大きい,となる(ここの解釈の部分少し不安定なので,少し再考必要).
また,こうした分析を行う前段階として,必ずグラフ等でx軸を時間変数,yを成績として各個人の成績を変化を示すようなグラフで視覚化する作業は必須であるので,そちらも必ず行う.
がんばれあたん